今回は2024年に解いた統計検定の過去問を解いてみました。ただし、私も受験生として挑戦したのがつい先日ですので、よくわかっていないところも大いにあると思います。参考になれば幸いですが、もし気になる箇所がありましたら真偽を確かめつつ参考にしていただけたらと思います。
問題自体は著作権の関係もあるのでこちらのページには載せません。解答に至るまでの考え方を上げていきます。例年であれば統計検定の公式ページから確認できるようになると思いますので、確認してみてください。(2025年1月12日14時時点では2023年の問題でした)
[5]は調整中です。
[5]も更新しました!(2025年3月9日)
[1]
まず、確率変数 $Y_i\ \ (i=1, … n)$ が以下のように与えられています。$ε_i$にはそれぞれ独立に正規分布$N(0, σ^2)$に従います。
$$ Y_i = \beta x_i+\epsilon_i $$
ここで$x_i$は正の定数と仮定があります。(試験本番で $x_i$ も確率変数と考えて意味の分からない計算をしたのはここだけの話です…)
今、$Y_i$の実現値、$y_i\ \ (i=1, … n)$が与えられたときの、$β$の対数尤度関数$l(\beta)$を求めないといけません。
初めに与えられた式をよく見ると、$\epsilon_i$について整理してあげれば、これが正規分布に従うことが示されているため、$\epsilon_i$たちについての同時確率密度関数は簡単にわかりそうですね。これを$\beta$についてみてあげたものが$β$の尤度関数だとわかれば解けたも同然です! $\epsilon_i$たちは互いに独立なので、それらの積をとってあげればよいです。
さっそく、$ε_1,…,ε_n$について、同時確率密度関数は
$$ f(ε_1,…,ε_n\ |\ β) = \prod^n_{i=1} \frac{1}{\sqrt{2\pi\sigma^2}} \exp \left(- \frac{\epsilon_i^2}{2 \sigma^2} \right) $$
で与えられます。最初の式から$\epsilon_i=y_i-\beta x_i$であることに注意すると、尤度関数$L(\beta)$は、
$$ L(β) = \prod^n_{i=1} \frac{1}{\sqrt{2\pi\sigma^2}} \exp \left(- \frac{(y_i-\beta x_i)^2}{2 \sigma^2} \right) $$
したがって、対数尤度関数$l(\beta)$は以下になります。
$$ l(\beta)=-\frac{n}{2}\log \left(2 \pi \sigma^2 \right)-\sum^n_{i=1} \frac{(y_i-\beta x_i)^2}{2 \sigma^2} $$
[2]
パラメータ$\beta$の最尤推定量を求める問題です。統計1級に向けて準備されている方であれば[1]が解ければ問題なく導けるでしょう。[1]で求めた対数尤度関数$l(\beta)$を$\beta$で微分して、それが0となるときの$\beta$を求めればよいのですね。
$$ \frac{d}{d\beta}l(\beta)=-\frac{1}{2 \sigma^2} \sum^n_{i=1} 2(Y_i-\beta x_i)(-x_i) = 0 $$
よって、求める$\hat \beta_{ML}$は、
$$ \hat \beta_{ML} = \frac{\sum^n_{i=1} Y_ix_i}{\sum^n_{i=1} x_i^2} $$
そして、この$\hat \beta_{ML}$が不偏推定量であることを示します。(こういった問題がスッと出されると一瞬わからなくなるのは私だけでしょうか…)
「不偏推定量である」=「期待値を計算して母数に一致する」ことを示せばよいので計算しましょう。といっても、$x_i$は正の定数ですから、
$$ E[Y_i]=E[\beta x_i+\epsilon_i]=\beta x_i $$
であることがわかれば、
$$ E[\hat \beta_{ML}] = \frac{\beta \sum^n_{i=1} x_i^2}{\sum^n_{i=1} x_i^2}=\beta $$
となり、不偏推定量であることが確かめられます。
[3]
一般的にパラメータ$\theta$のフィッシャー情報量$I_n(\theta)$は以下のように表せます。ここで、$\mathbf \it X$は$n$個の確率変数の組$X_1,…X_n$を表します。
$$ I_n(\theta)=E\left[ \left\{ \frac{d}{d\theta} \log f_n(X\ |\ \theta) \right\}^2 \right]=-E\left[ \frac{d^2}{d\theta^2} \log f_n(X\ |\ \theta) \right] $$
どちらでも計算すれば求まるのですが、基本的には二階微分を用いて表したものがすぐに計算可能です。[2]で最尤推定量を求めるときに一階微分のものは求まっているので、それをさらに微分して、期待値を計算して符号に気を付ければ大丈夫です。
$$ \frac{d^2}{d\beta^2}l_n(\beta)=-\frac{d}{d\beta}\frac{1}{2 \sigma^2} \sum^n_{i=1} 2(Y_i-\beta x_i)(-x_i) = -\frac{1}{\sigma^2}\sum^n_{i=1}x_i^2 $$
よって、フィッシャー情報量$I_n(\beta)$は、($x_i$は定数なので、期待値をとってもそのままですね)
$$ I_n(\beta)=-E\left[-\frac{1}{\sigma^2}\sum^n_{i=1}x_i^2\right]=\frac{\sum^n_{i=1}x_i^2}{\sigma^2} $$
クラメール・ラオの下限は、フィッシャー情報量の逆数で与えられるので、
$$ \frac{1}{I_n(\beta)} = \frac{\sigma^2}{\sum^n_{i=1}x_i^2} $$
が解答になります。
[3]までは尤度関数を求めて、最尤推定量を求めて、フィッシャー情報量やクラメール・ラオの下限を出すといった、問題演習としてはかなりオーソドックスな問題かなと思います。
[4]
以下で与えられた推定量の期待値と分散を求める問題です。
$$ \tilde \beta=\frac{\sum^n_{i=1}Y_i}{\sum^n_{i=1}x_i} $$
[2]と同様ですが、$E[Y_i]=E[\beta x_i+\epsilon_i]=\beta x_i$ だということがわかっていれば期待値はすぐに求まります。
$$ E[\tilde \beta] =\frac{\beta \sum^n_{i=1}x_i}{\sum^n_{i=1}x_i}=\beta $$
となり、与えられた推定量も不偏推定量になりますね。
分散もほとんど同じです。$Var[Y_i] = Var[\beta x_i+\epsilon_i]=Var[\epsilon_i]=\sigma^2$ であることがわかります。また、$\epsilon_i$はそれぞれ独立であるため、$Var[\sum^n_{i=1} Y_i] = \sum^n_{i=1} Var[Y_i]$ が成り立ちます。(忘れがちかもしれないですが、独立でない場合は異なる項$[Y_i, Y_j]$同士の相関係数を考慮して総和に含めないといけません)
$$ Var[\tilde \beta] = Var\left[\frac{\sum^n_{i=1}Y_i}{\sum^n_{i=1}x_i}\right]=\frac{\sum^n_{i=1}Var[Y_i]}{(\sum^n_{i=1}x_i)^2}=\frac{n\sigma^2}{(\sum^n_{i=1}x_i)^2} $$
となります。分散を扱うときに、係数は2乗して外に出すことに注意してください(($\sum^n_{i=1}x_i)^2$の部分です)。
[5]
調整といって逃げていましたがまとめてみました…。2024年統計数理の中では最も難しい部類に入る設問ではいないでしょうか?([3]の計算力が試される問題とどっちが難しいだろうか…)。
解答書いてみますが、不十分な点や誤りもあるかもしれないです…。
まずはフンワリと理解してみましょう。
最尤推定量である $\beta_{ML}$の分散はクラメール・ラオの下限に達していて、不偏推定量の中では最小の分散を持つ推定量です。一方、 $\tilde \beta$の分散の値は $\hat \beta_{ML}$とは異なりますが $\tilde \beta$も不偏推定量です。よって $\hat \beta_{ML}$の分散よりは大きいです。
これらの推定量で推定することを考えた場合に、分散の大小で以下のようになると考えられます。帰無仮説通り $\beta=0$である場合を考えると、どちらも0を中心とした分布となりますが、その裾の広がり方が違います。図では正規表現を想定して書いていますが、 $\hat \beta_{ML}, \tilde \beta$ともに正規分布に従う $\varepsilon_i$を足し合わせていることからそのようになることがわかります。
これら二つの分布を用いて、例えば上側5%点を超える場合に棄却するような検定を考えてみましょう。 $\hat \beta_{ML}, \tilde \beta$を用いた場合に $c_{ML}, \tilde c$を超えたら棄却するとします。すなわち、
$$ P(\hat \beta_{ML} \ge c_{ML}\space|\space\beta=0)=P(\tilde \beta \ge \tilde c\space|\space\beta=0) = 0.05 $$
とあらわされます。 $\tilde \beta$を用いたときは $\hat \beta_{ML}$よりも分散が大きいので、以下のように図にしてみると $c_{ML} \le \tilde c$ になりそうだなとわかると思います。
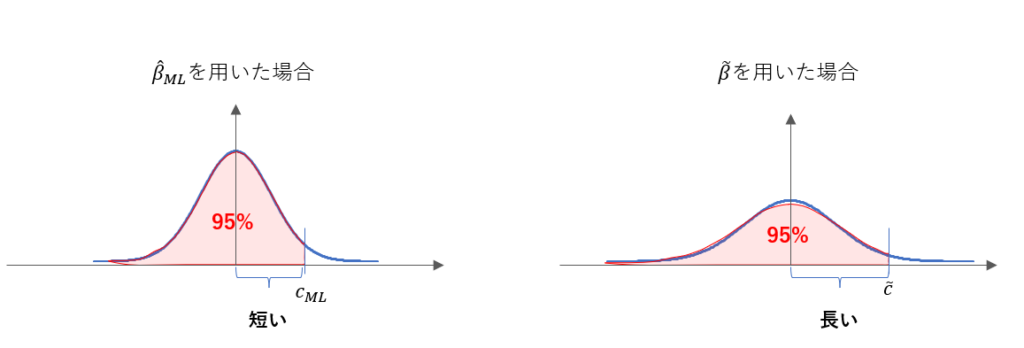
以上のようにして、「棄却域が $\tilde \beta$を用いたときの方が厳しそうだな…」、というところまでくれば、何とかそれを数式に起こしてあげて解答できるかもしれないです。もちろん、実際に $\beta>0$ として、検出力まで図解しないと何とも言えないではないか、という話はあるのですが、いったん指針としては良しとすることにします。
それでは実際に式に起こしてみましょう。
目標は公式の略解にもあるように、以下の式を示すことです。
$$ P(\hat \beta_{ML} \ge c_{ML}\space|\space\beta=\beta_1) \ge P(\tilde \beta \ge \tilde c\space|\space\beta=\beta_1) $$
先ほどの例では上側5%点を考えましたが、一般化して $\alpha$としましょう。
$\hat \beta_{ML}$を用いたときの棄却域の下限 $c_{ML}$を求めてみましょう。
$$ P(\hat \beta_{ML} \ge c_{ML}\space|\space\beta=0) $$ $$ = P\left(\frac{\hat \beta_{ML}-0}{\sqrt {Var[\hat \beta_{ML}]}} \ge \frac{c_{ML}-0}{\sqrt {Var[\hat \beta_{ML}]}}\space|\space\beta=0\right) $$ $$ = P\left(z \ge \frac{c_{ML}}{\sqrt {Var[\hat \beta_{ML}]}}\space|\space\beta=0\right) = \alpha $$
ここで、 $z$は標準正規分布にしたがう確率変数です。標準正規分布の上側 $\alpha$%点を $z_\alpha$とすれば、
$$ \frac{c_{ML}}{\sqrt {Var[\hat \beta_{ML}]}} = z_\alpha $$
$$ c_{ML} = z_\alpha\sqrt {Var[\hat \beta_{ML}]} $$
とあらわすことができます。
検出力を考えるために、 $\beta=\beta_1 \space (>0)$の場合で考えましょう。
$$ P(\hat \beta_{ML} \ge c_{ML}\space|\space\beta=\beta_1) $$ $$ = P\left(\frac{\hat \beta_{ML}-\beta_1}{\sqrt {Var[\hat \beta_{ML}]}} \ge \frac{c_{ML}-\beta_1}{\sqrt {Var[\hat \beta_{ML}]}}\space|\space\beta=\beta_1\right) $$ $$ = P\left(z \ge \frac{c_{ML}-\beta_1}{\sqrt {Var[\hat \beta_{ML}]}}\space|\space\beta=\beta_1\right) $$ $$ = P\left(z \ge z_\alpha \space – \space \frac{\beta_1}{\sqrt {Var[\hat \beta_{ML}]}}\space|\space\beta=\beta_1\right ) $$
この確率が $\hat \beta_{ML}$を用いた場合の検出力です。 $\tilde \beta$を用いたときも同様に考えればよく、その検出力は同じ式変形で得られます。 $\tilde c$は、
$$ \tilde c = z_\alpha\sqrt {Var[\tilde \beta]} $$
検出力は、
$$ P\left(z \ge z_\alpha \space – \space \frac{\beta_1}{\sqrt {Var[\tilde \beta]}}\space|\space\beta=\beta_1\right ) $$
となります。いま、 $Var[\hat \beta_{ML}] \le Var[\tilde \beta]$ですから、
$$ z_\alpha \space – \space \frac{\beta_1}{\sqrt {Var[\hat \beta_{ML}]}} \le z_\alpha \space – \space \frac{\beta_1}{\sqrt {Var[\tilde \beta]}} $$
となります。よって、検出力同士を比較すると、
$$ P\left(z \ge z_\alpha \space – \space \frac{\beta_1}{\sqrt {Var[\hat \beta_{ML}]}}\space|\space\beta=\beta_1\right ) \ge P\left(z \ge z_\alpha \space – \space \frac{\beta_1}{\sqrt {Var[\tilde \beta]}}\space|\space\beta=\beta_1\right ) $$
となります。したがって、 $\hat \beta_{ML}$を用いたときの方が検出力が高くなることがわかります。ちなみに、最初に図で示した、「棄却域が $\tilde \beta$を用いたときの方が厳しそうだな…」というのは、 $c_{ML}$と $\tilde c$の式に表れています。分散の平方根がかかっているため、より分散の大きい $\tilde \beta$を用いたときの方が棄却域の下限が高かったのですね。
以上で、ようやく2024年統計数理大問1の解説を終わります。途中、[5]は保留にするなど難しい問題でしたが、しっかり考えてみるとよい復習になりました。本番でも[4]まで解けたということもあり、[5]を粘りたくなりましたが早めに切り上げて正解でした。定性的なことを記述しても部分点が入りそうな気がする?ので、最初はそれくらいの記述にとどめておいて、時間が余れば戻ってくるのがよいでしょう。おそらく[4]までの解答できるかどうかで合否が分かれたと思います。

コメントを残す